10 探索性数据分析

10.1 简介

本章将介绍如何通过可视化和数据转换系统化地探索数据，这一过程在统计学中称为探索性数据分析（Exploratory Data Analysis, EDA）。EDA是一个迭代循环的过程，包含以下步骤：

提出问题：针对数据生成初步问题；
探索答案：通过可视化、数据转换和建模寻找答案；
迭代优化：根据发现的问题调整或生成新问题。

EDA是数据分析的核心环节，能帮助评估数据质量。例如，数据清洗本质上就是EDA的应用：通过质疑数据是否符合预期，利用可视化、转换和建模工具识别并解决问题。

10.2 问题的艺术

在EDA过程中，核心目标是理解数据，而提问是引导探索的最佳工具。每个问题都会聚焦到数据的特定方面，进而选择恰当的可视化、模型或数据转换方法。

EDA本质上是创造性过程，提出高质量问题的关键在于追求问题数量。虽然由于尚未了解数据中隐藏信息，初期问题可能较肤浅，但每个新问题都会揭示新视角。通过连续追问可逐步深入数据。

提问没有固定模板，但以下两类问题一般最有研究价值：

变异（Variation）

例如：某变量的分布形态如何？是否存在异常值？

“顾客年龄范围是多少？80岁的记录是真实数据还是输入错误？”
共变（Covariation）

例如：两个变量是否存在关联？关联强度如何？

“产品销量与广告支出是否同步变化？季节性影响是否显著？”

10.3 变异

变异（Variation）指变量在不同测量中取值的波动现象。现实中所有连续变量都会存在变异，结果也会因微小误差而不同。理解变异的关键在于可视化的值分布。

以钻石重量（carat）为例，通过直方图观察其分布：

# 全数据集直方图（右偏分布）
ggplot(diamonds, aes(x = carat)) +
  geom_histogram(binwidth = 0.5)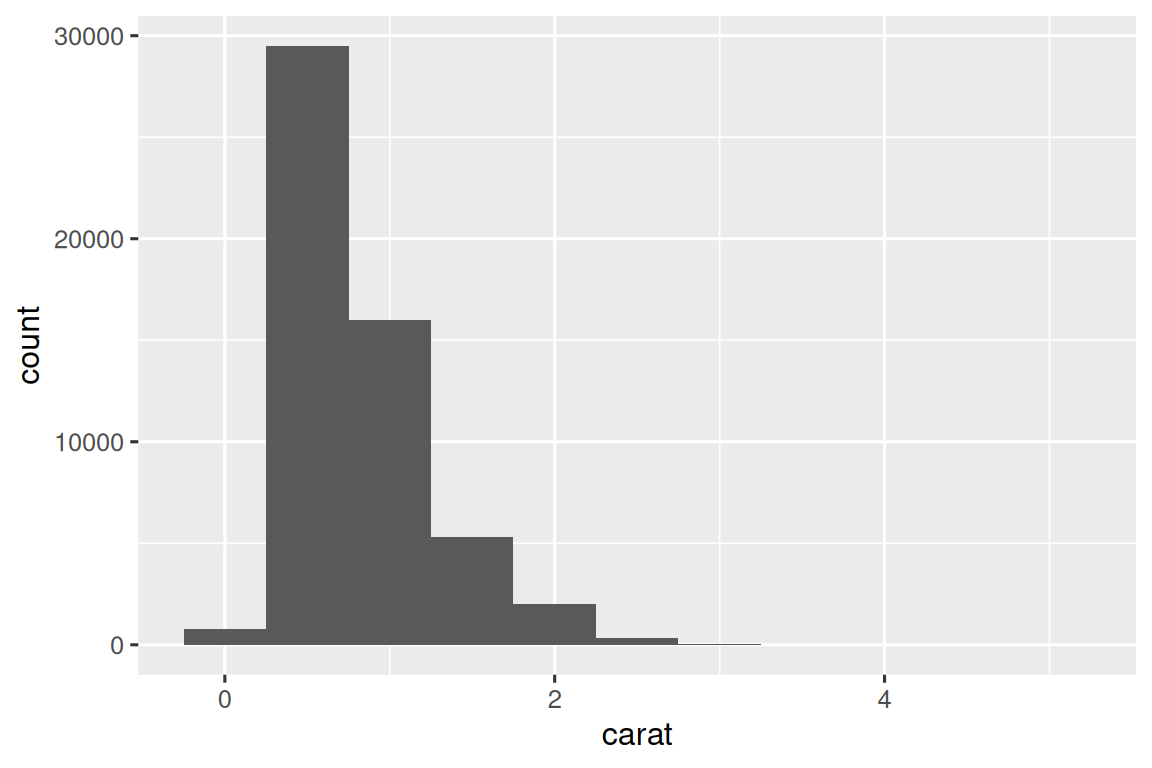

# 聚焦小克拉钻石（窄binwidth揭示细节）
smaller <- diamonds |>
  filter(carat < 3)

ggplot(smaller, aes(x = carat)) +
  geom_histogram(binwidth = 0.01)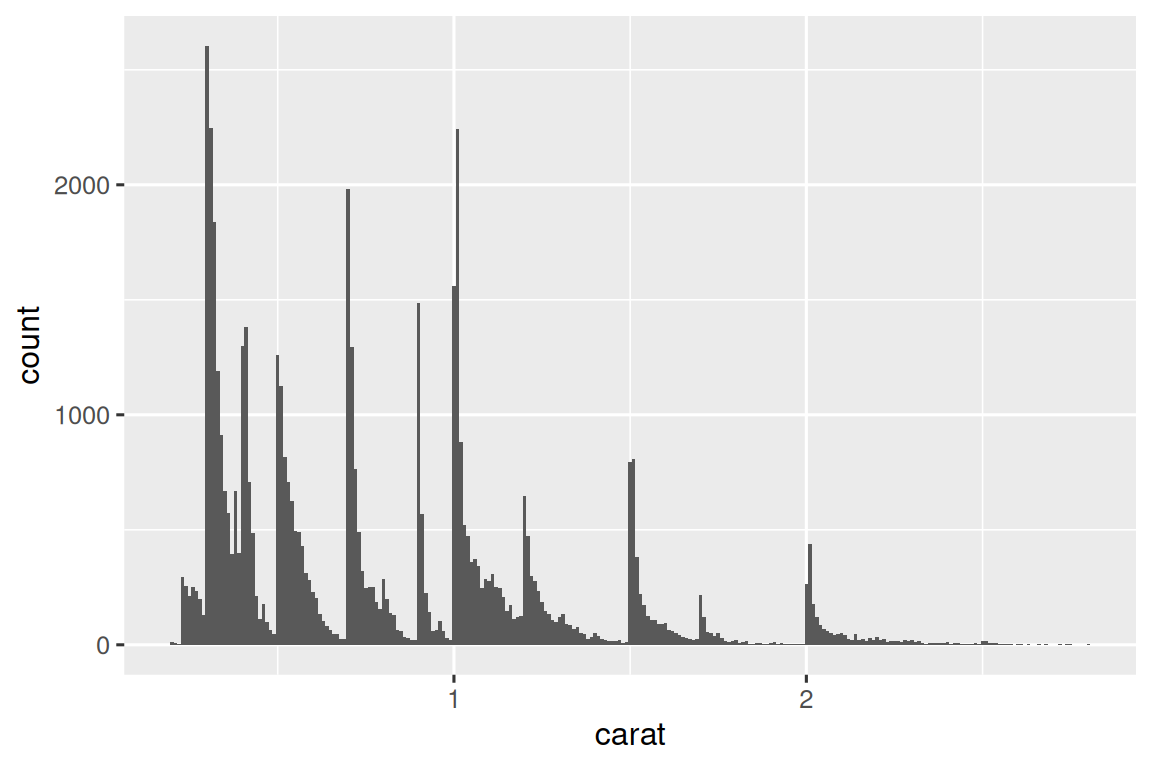

根据可视化图形，我们就可以进一步观察与追问。比如：

峰值现象

为什么克拉数为整数或常见分数（如0.5、1）的钻石更多？

可能钻石切割标准或消费者偏好导致特定重量更常见。
右偏特征

每个峰值右侧的钻石为何比左侧多？

可能切割时倾向于略微超重而非不足。

诸如此类。

图中若出现异常值，可能是错误数据或某些特殊现象。以钻石尺寸（y轴长度）为例：

# 基础直方图（异常值被掩盖）
ggplot(diamonds, aes(x = y)) + 
  geom_histogram(binwidth = 0.5)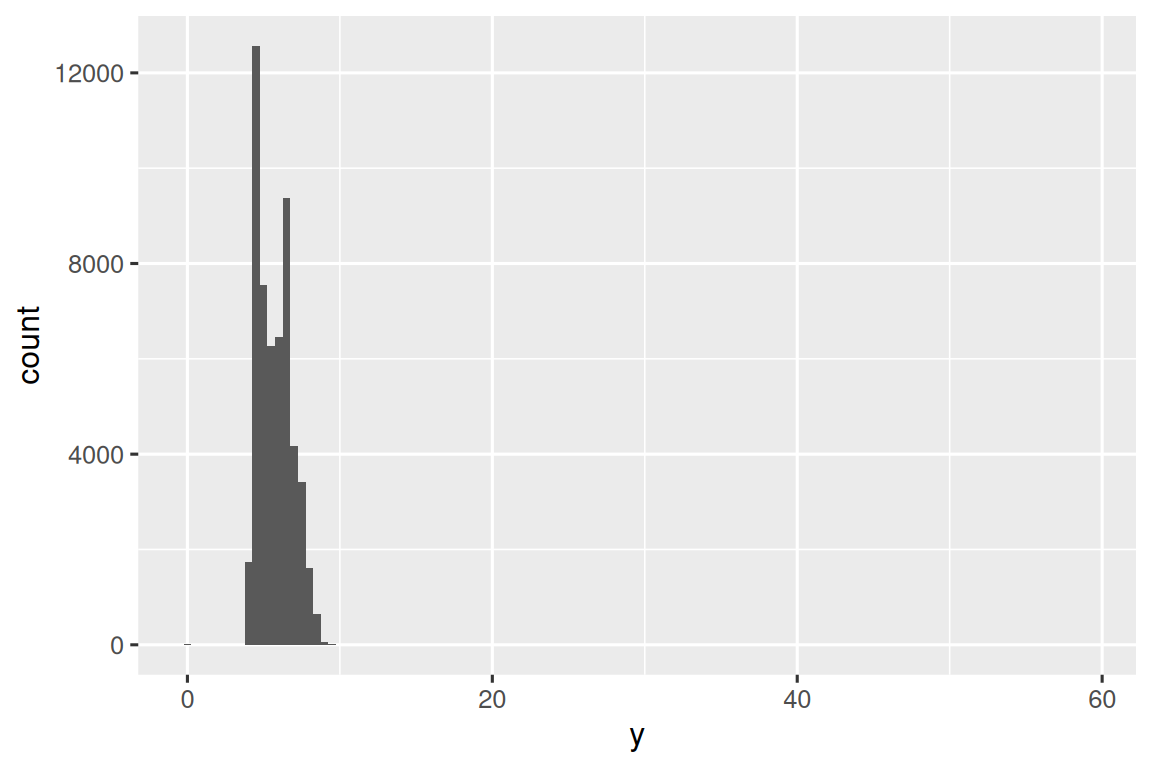

# 聚焦y轴低频区域（暴露出异常）
ggplot(diamonds, aes(x = y)) + 
  geom_histogram(binwidth = 0.5) +
  coord_cartesian(ylim = c(0, 50))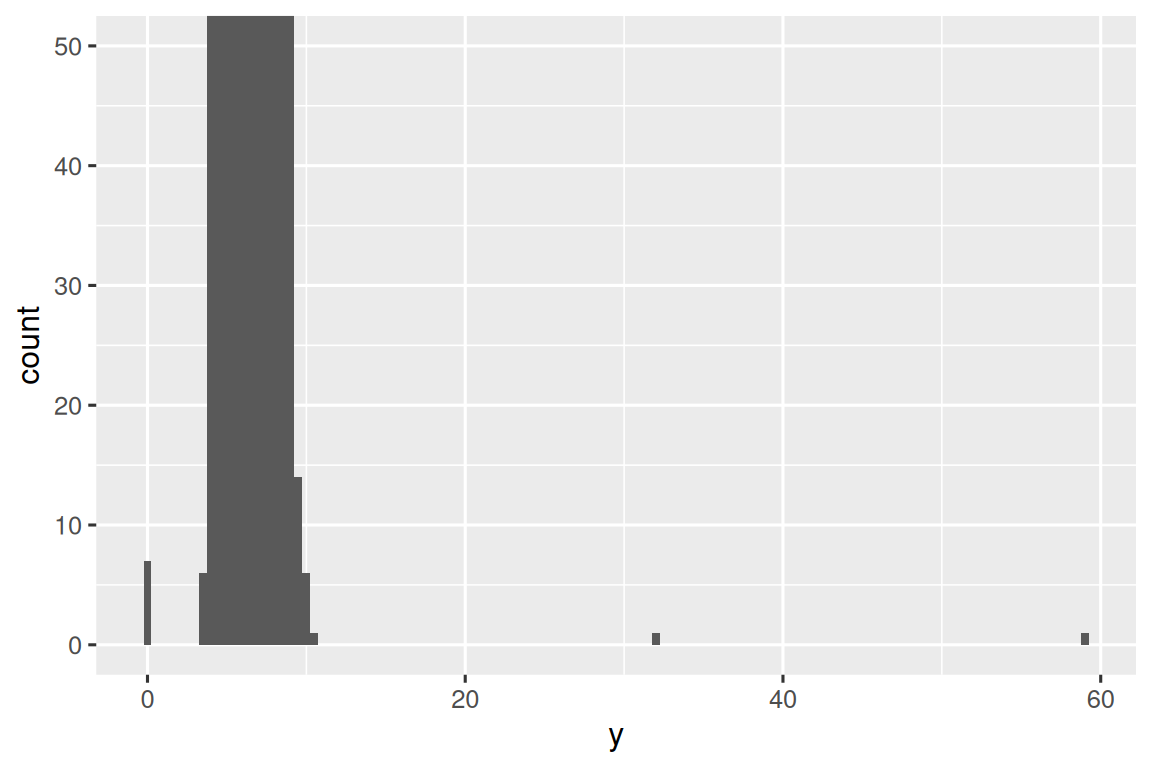

# 根据图形提取异常记录
unusual <- diamonds |> 
  filter(y < 3 | y > 20) |> 
  select(price, x, y, z) |>
  arrange(y)

提取完异常值，可按照以下思路针对性分析。

零值

尺寸为0mm的钻石（y=0）显然是数据错误，应转换为NA。
极端值

长达30mm+的钻石若价格不足万元，可能需核实：
- 是否单位错误（如英寸误录为毫米）
- 是否测量设备故障

通过这种分析，我们不仅发现了数据质量问题（如零值），还可能识别出特殊钻石类别（如超大但低价的异常记录），为进一步处理提供方向。

10.4 异常值处理

数据中的异常值需要继续处理，有两种方式。

直接删除整行

diamonds2 <- diamonds |> 
  filter(between(y, 3, 20))

但是存在隐患，毕竟单个变量的异常不代表整行数据无效。

替换为缺失值(NA)

diamonds2 <- diamonds |> 
  mutate(y = if_else(y < 3 | y > 20, NA, y))

这一方法就更合理，能够保留其他变量的有效信息。

排除缺失值后再次可视化，ggplot2默认移除缺失值并给出警告：

ggplot(diamonds2, aes(x = x, y = y)) + 
  geom_point()
#> Warning: Removed 9 rows containing missing values or values outside the scale range

可通过na.rm = TRUE隐藏警告：

ggplot(diamonds2, aes(x = x, y = y)) + 
  geom_point(na.rm = TRUE)

而有时缺失值本身也具有意义。例如航班数据中，dep_time为NA时，表示航班取消。

10.5 共变

共变（Covariation）描述变量间的协同变化关系，是探索数据多维模式的核心工具。本节探索钻石价格与切工质量的关系，通过两种可视化方法揭示反常现象及其原因。

频率多边形（Density标准化）

我们首先进行初次尝试：

ggplot(diamonds, aes(x = price)) + 
  geom_freqpoly(aes(color = cut), binwidth = 500, linewidth = 0.75)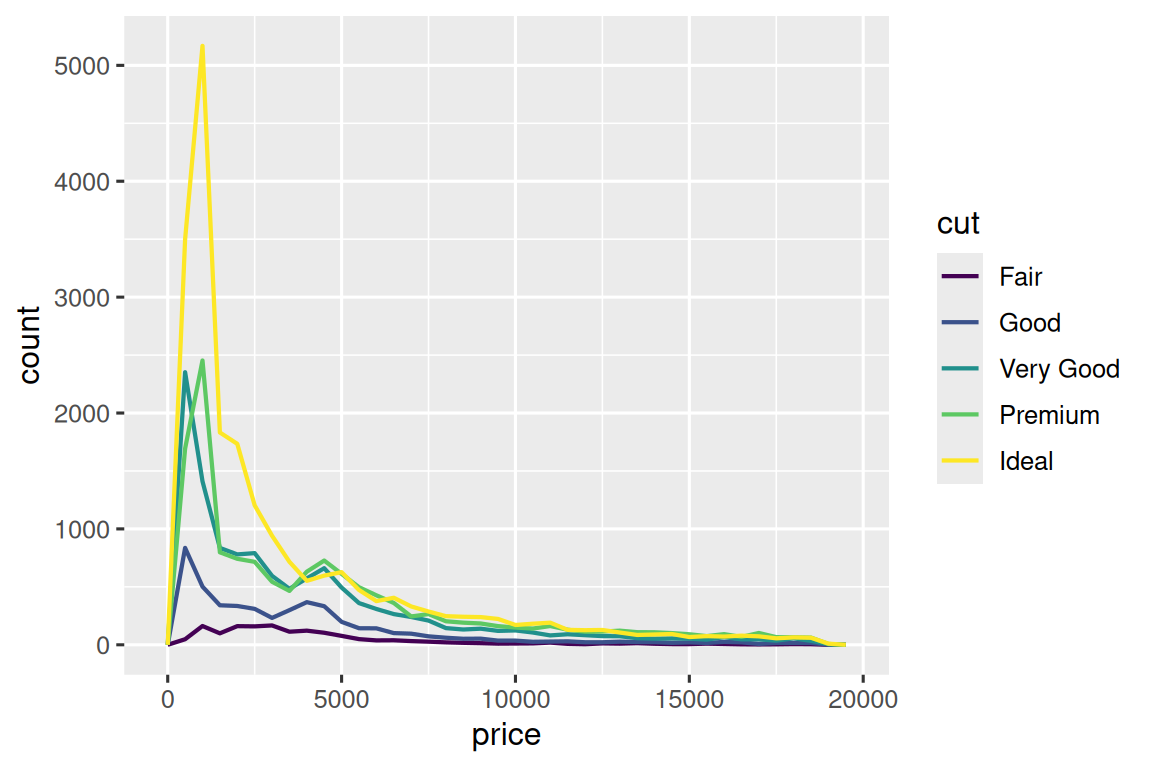

这张图存在两点问题：

不同切工等级的样本量差异大（如Ideal切工钻石最多），导致频数难以直接比较。
图形重叠严重，无法清晰观察分布形态差异。

如下改进：

ggplot(diamonds, aes(x = price, y = after_stat(density))) + 
  geom_freqpoly(aes(color = cut), binwidth = 500, linewidth = 0.75)

将y轴从绝对计数转换为相对密度，使得每条曲线下的面积均为1。

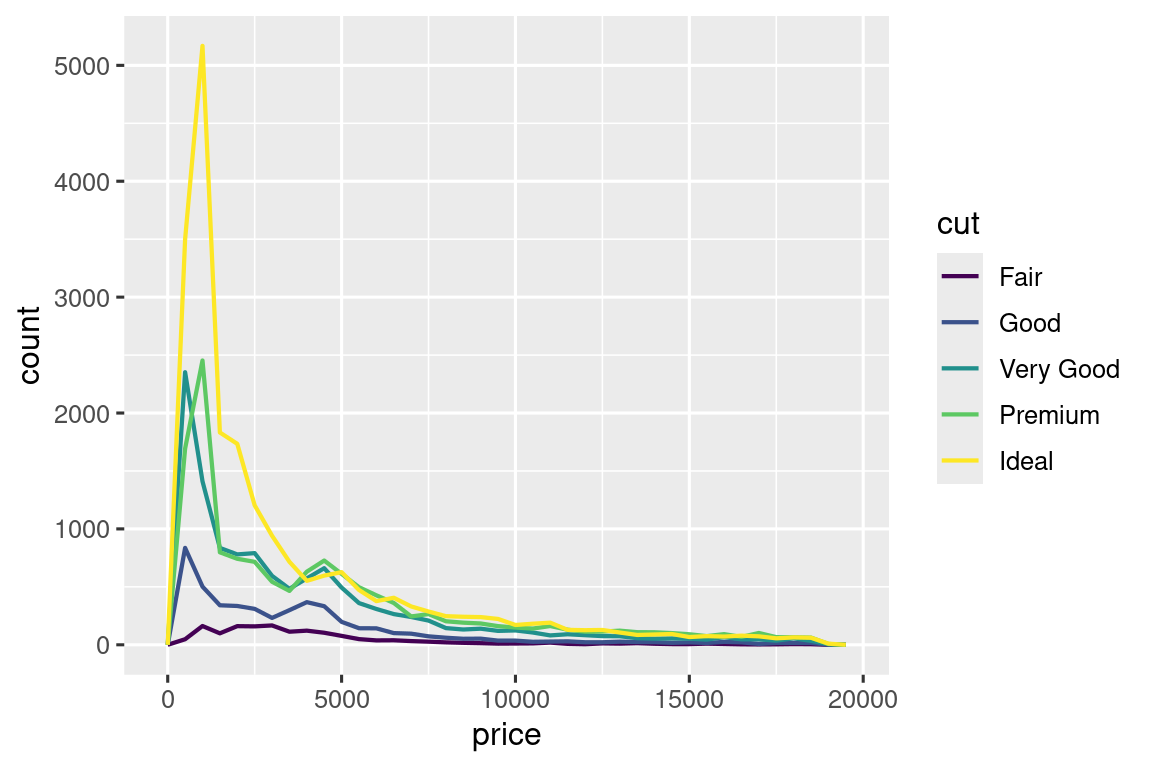
这样便可进行分析：

Fair切工（最低等级）的钻石价格密度分布右移，均值最高，较为反常。
其他切工等级在1500美元附近出现高峰。

箱线图

ggplot(diamonds, aes(x = cut, y = price)) +
  geom_boxplot()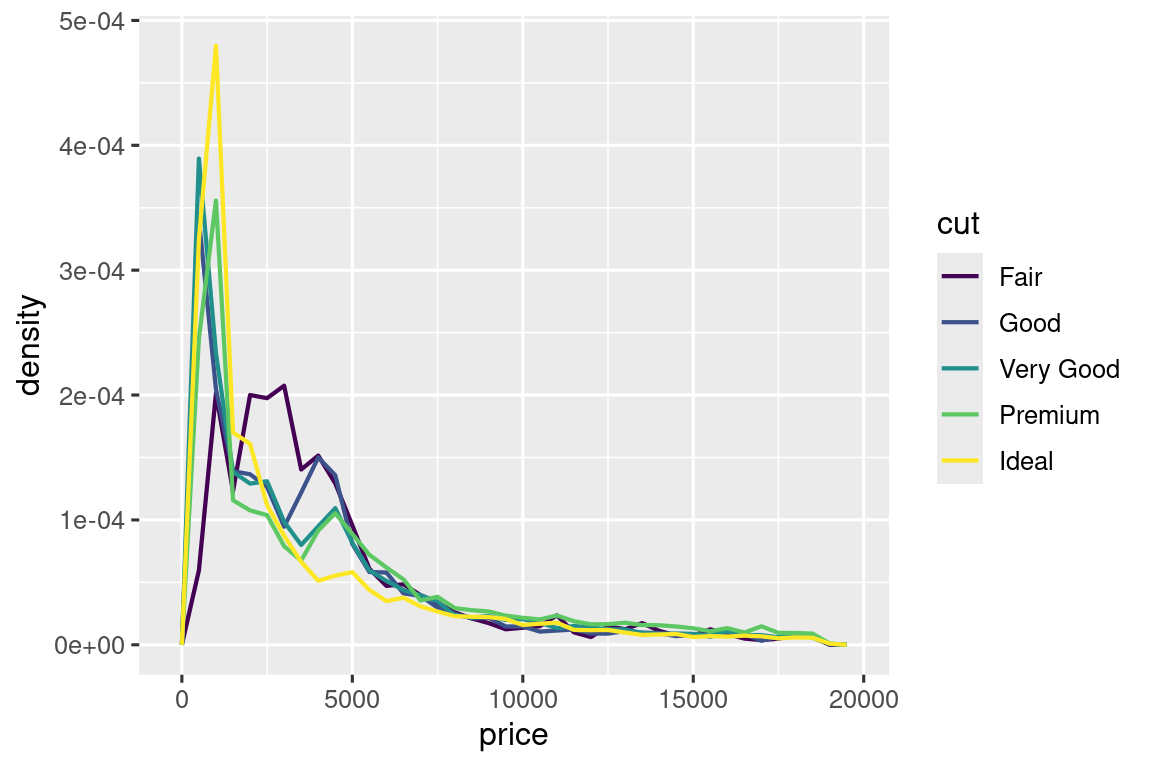

分析可得：

中位数价格：Fair > Good > Very Good > Premium > Ideal（随切工等级提升而下降）。
分布形态：所有切工等级均右偏，但Fair切工的离群点更多。

针对箱线图，还有一些扩展技巧如下。

示例：车辆油耗（hwy）按车型（class）分类

# 默认无序排列
ggplot(mpg, aes(x = class, y = hwy)) + geom_boxplot()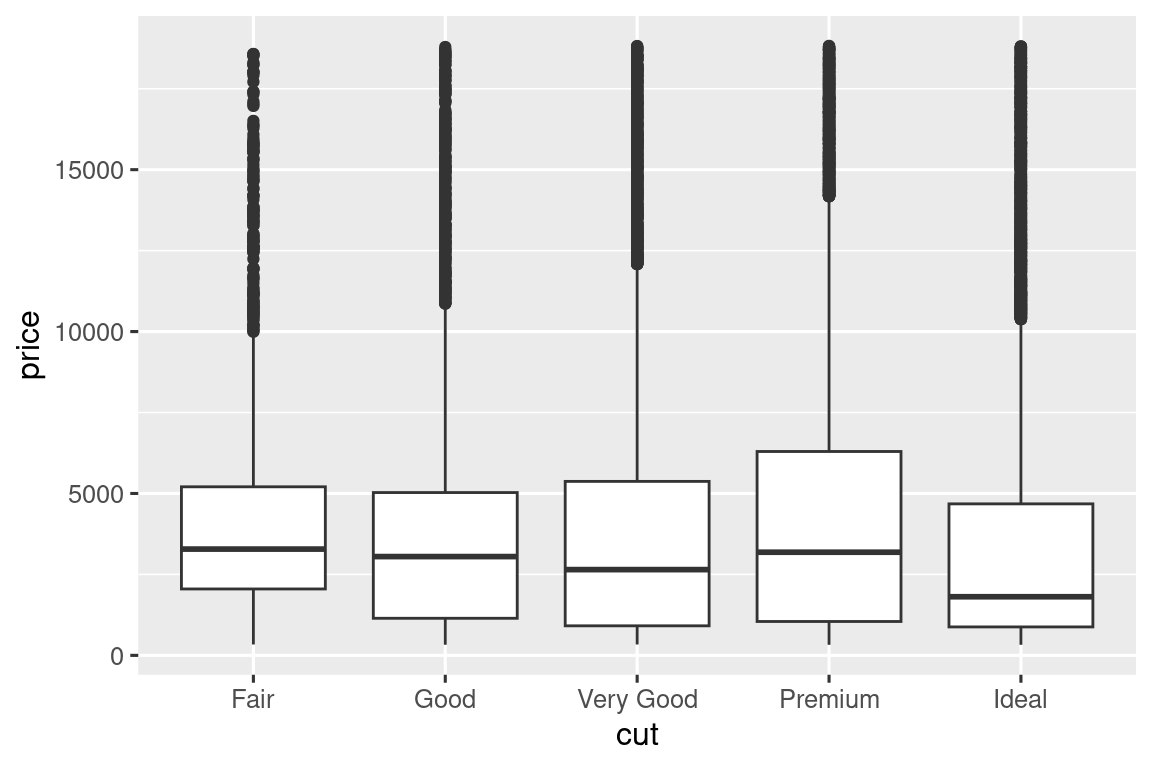

# 按中位数排序
ggplot(mpg, aes(x = fct_reorder(class, hwy, median), y = hwy)) +
  geom_boxplot()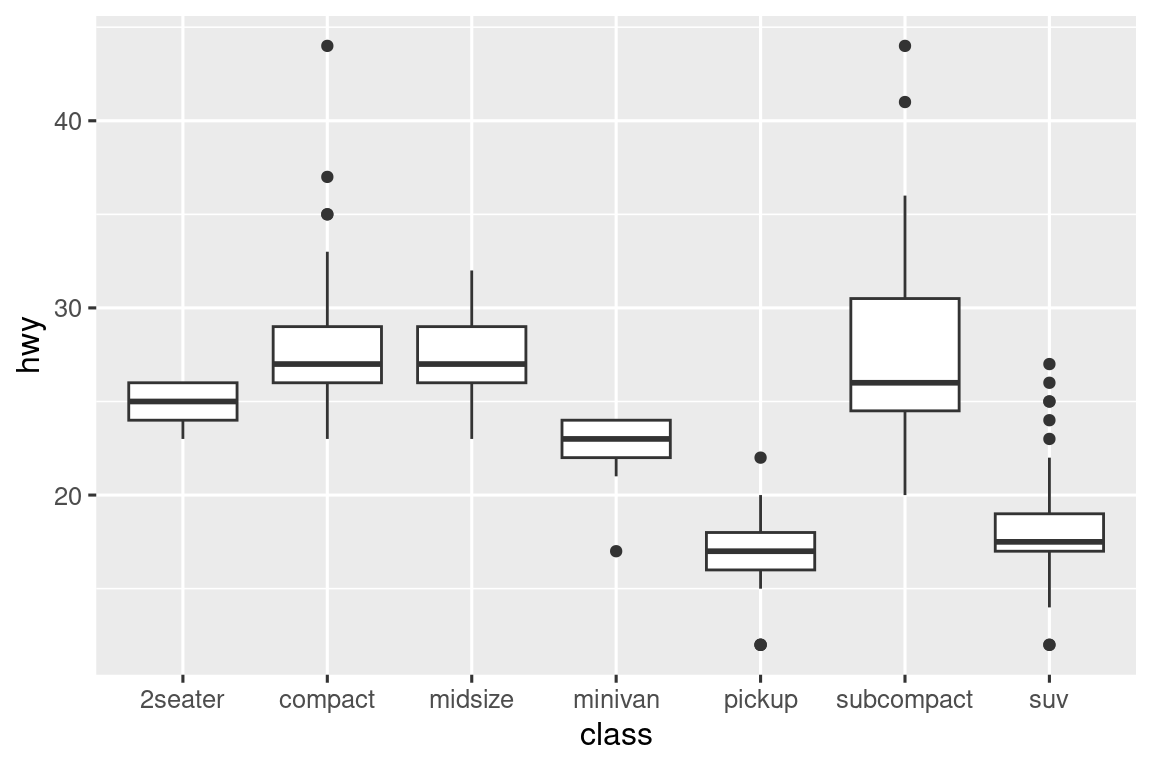

# 若名称过长，可翻转坐标轴
ggplot(mpg, aes(x = hwy, y = fct_reorder(class, hwy, median))) +
  geom_boxplot()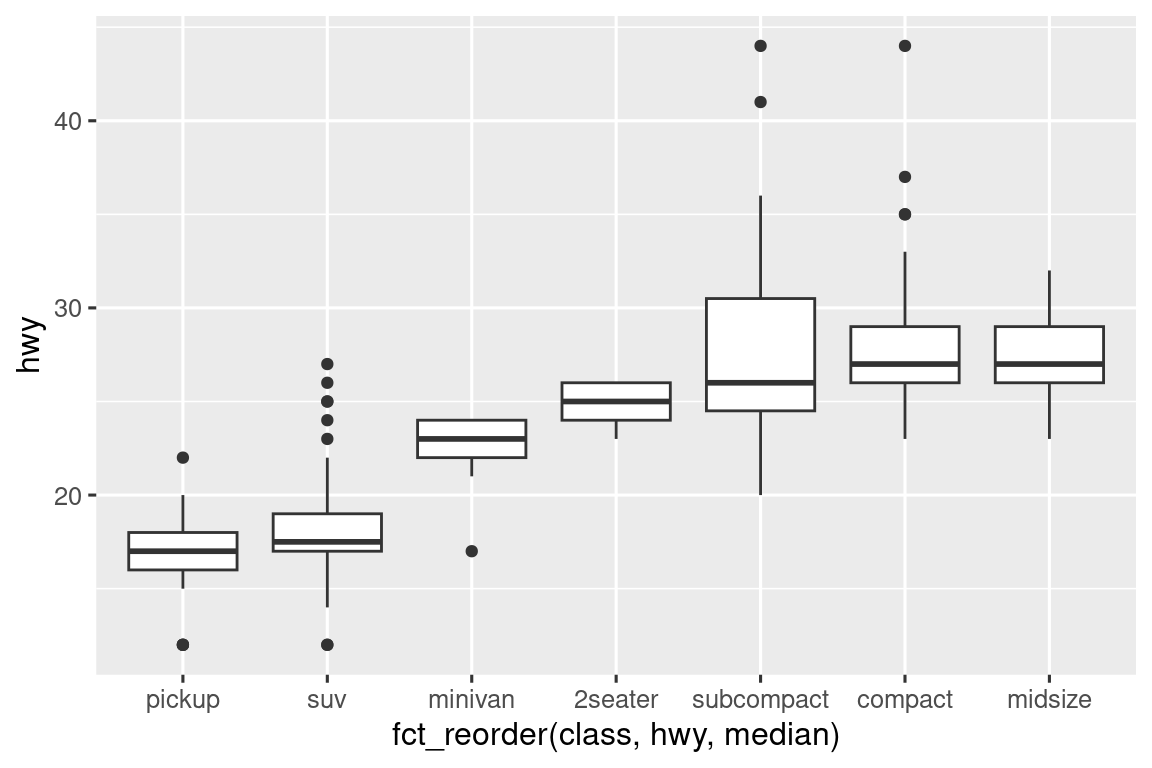

下面对变量关系进一步分析，但首先应确认变量类型。

若要对两个分类变量的关系进行分析，有以下两种方法。

气泡图（geom_count()）
```
ggplot(diamonds, aes(x = cut, y = color)) +
  geom_count()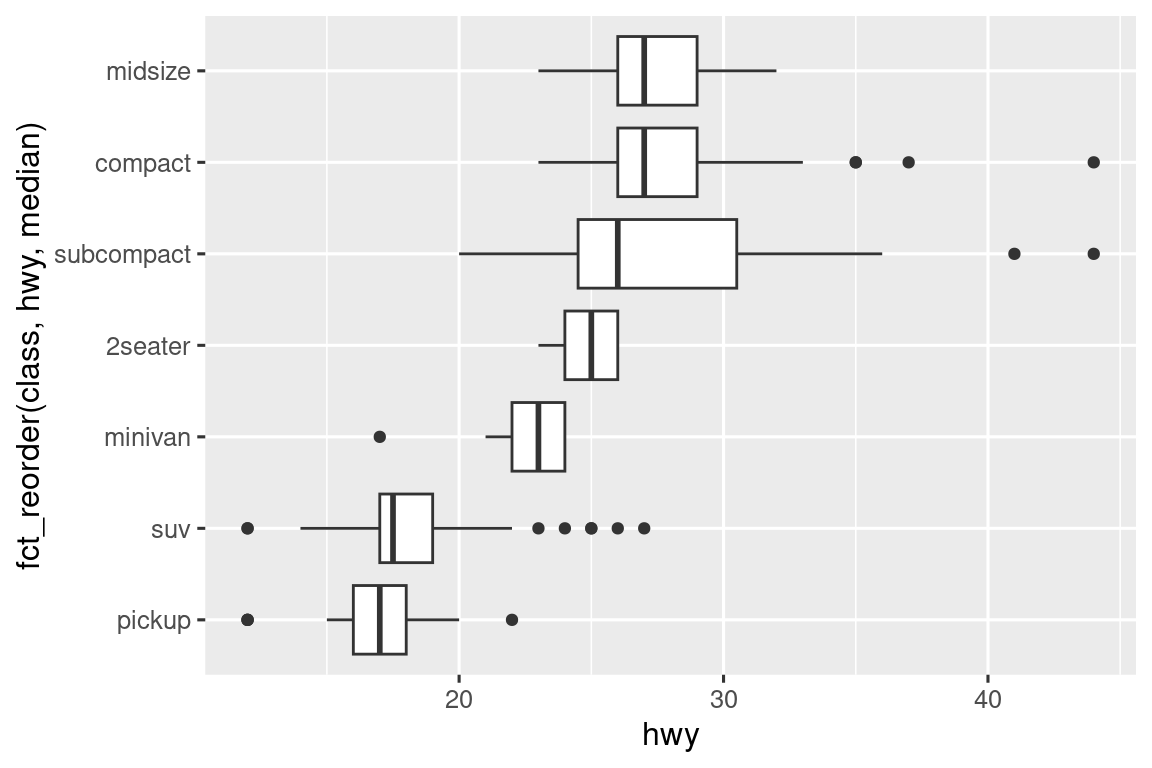
```
每个气泡大小表示组合频数（如G色Ideal切工钻石最多）。虽然直观，但当类别过多时，气泡可能重叠。
热图（geom_tile()）
```
diamonds |> 
  count(color, cut) |>  
  ggplot(aes(x = color, y = cut, fill = n)) +
  geom_tile() +
  scale_fill_viridis_c()  # 优化颜色梯度
```
颜色深浅直观反映频数差异，适合展示高维组合。

例如根据上图可分析出：
- Ideal切工在D-G色中更常见，而J色几乎无Ideal切工。
- Fair切工在低色级（I-J）占比更高。

若要对两个数值变量的关系进行分析，有以下两种方法。

过绘制（Overplotting）

ggplot(smaller, aes(x = carat, y = price)) + 
  geom_point(alpha = 0.01)  # 调整透明度，揭示数据密集区域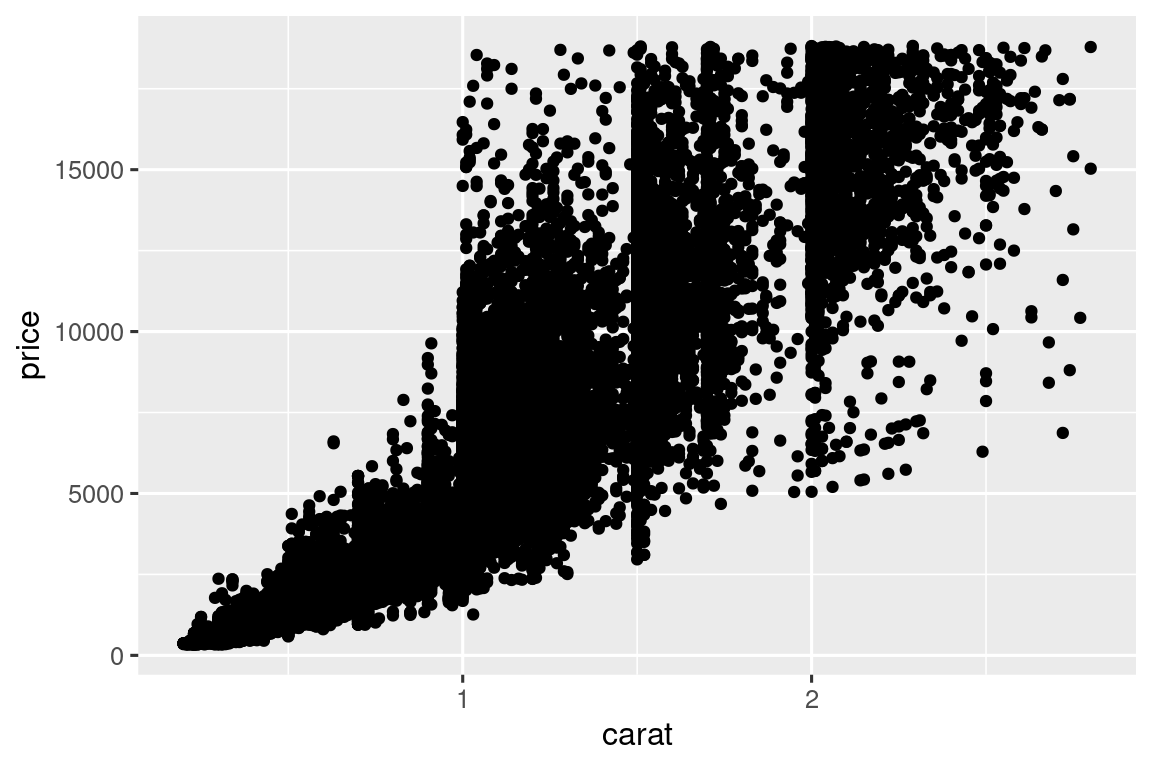

二维分箱

矩形分箱（geom_bin2d()）

ggplot(smaller, aes(x = carat, y = price)) +
  geom_bin2d() +
  scale_fill_gradient(low = "lightblue", high = "darkred")

六边形分箱（geom_hex()）

library(hexbin)
ggplot(smaller, aes(x = carat, y = price)) +
  geom_hex()  # 相邻单元过渡更自然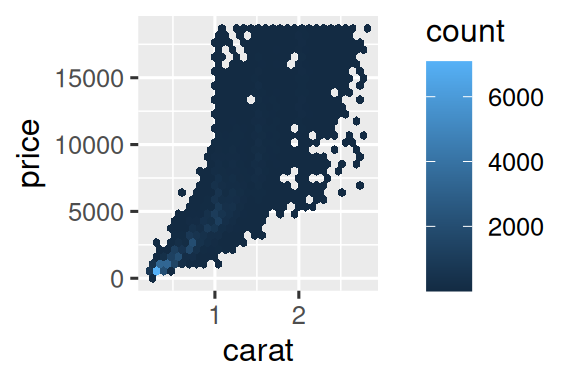

离散化+箱线图

ggplot(smaller, aes(x = carat, y = price)) + 
  geom_boxplot(aes(group = cut_width(carat, 0.1)), varwidth = TRUE)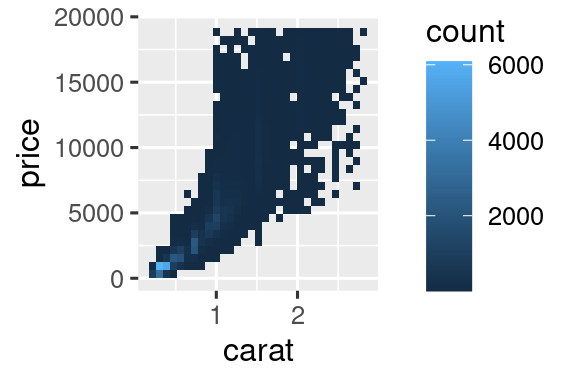

关键参数

cut_width(x, width)：按固定宽度分箱。

varwidth = TRUE：箱宽反映样本量。

10.6 模式与模型

当数据中出现系统性关系时，它会表现为某种模式(pattern)。发现模式后，需追问以下问题：

该模式是否因巧合产生？
如何描述该模式暗示的关系？
这种关系的相关性强度如何？
是否有其他变量影响该关系？
在不同数据子组中，该关系是否不同？

要解决以上问题，我们需创建模型(model)。

比如现在对钻石进行分析，其价格（price）同时受克拉（carat）和切工（cut）影响，而克拉与切工又存在关联（高切工等级的钻石通常较小）。直接观察cut与price的关系会产生误导，因此我们建立预测模型，用克拉预测价格，提取残差并分析。残差会反映出反常的价格波动，此时再探索切工的影响。

library(tidymodels)

# 对数变换后建模（更适合指数关系）
diamonds <- diamonds |>
  mutate(
    log_price = log(price),
    log_carat = log(carat)
  )

# 拟合线性模型
diamonds_fit <- linear_reg() |>
  fit(log_price ~ log_carat, data = diamonds)

# 计算残差并逆变换
diamonds_aug <- augment(diamonds_fit, new_data = diamonds) |>
  mutate(.resid = exp(.resid))  # 残差还原为原始价格尺度

# 可视化残差与克拉的关系
ggplot(diamonds_aug, aes(x = carat, y = .resid)) + 
  geom_point(alpha = 0.1) +
  labs(y = "Price Residuals (adjusted for carat)")

根据可视化图形可发现，大克拉钻石的残差普遍更低。

可见，创建模型后，更方便进一步确认变量间的模式。